Convex Hull

I want to find the convex hull of some set of points in  (a euclidean space of arbitrary dimension). I am hoping that this will be an interesting programming exercise, and that it will provide some insight into the properties of higher dimensions.

Definition

The Convex Hull of a set S is the smallest convex set that contains all elements of S. So much for the mathematical definition. Intuitively, we can think of the convex hull as the shape of a rubber band that encloses all points in S. 

Example of the convex hull of a set of points. 

A Simple Test

When starting out, I thought about explicitly constructing the convex hull. This is indeed something we will get to later. By explicitly constructing the hull, I mean finding the linear subspaces that constitute it. In the example above, that would imply finding the line equations of the red lines. However, it struck me that this is not necessary if all we want is to test whether some given point is inside the convex hull or not. There is a way to do it by solving a single linear programming problem. We use the following fact:

A vector u is in the convex hull of a set of points V if u can be expressed as a convex linear combination of the vectors in V. That is:

such that:

.

This can be readily formulated as a linear program, where u and V are given, and the lambdas are variables. The code:

This works beautifully in 2D:

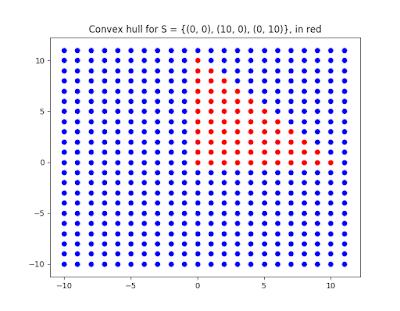Convex hull for the set of points (0, 0), (1, 0), (0, 1), marked with red dots. Sampled in the integers. 

Convex hull (red) of random points (green) sampled in the integers. 

Volume of Convex Hull using Monte Carlo

One question I had was: "suppose we take 10 random points sampled from the unit cube, what is the expected volume of their convex hull?". This requires a nested simulation. On the highest level, we need to sample a lot of 10-point sets and measure their volumes. And for each volume that we want to measure, we need to sample a lot of points to get an accurate Monte Carlo estimate of the volume. Some initial tests:

dim | volume: 10 points | volume: 100 points
2D  | 0.42              | 0.88
3D  | 0.14              | 0.69
4D  | 0.035             | 0.45

What can we say from this? Not much more than that the average coverage decreases as the number of dimensions increase.