Minesweeper pt. 3: more gameplay

See part 1 for a description of Tile Domination and Gradient.

Adding the feature from part 2, that guarantees that the instances are solvable makes the game much more satisfying. With this knowledge, I could spend all the time thinking of clever inferences, instead of wondering whether the instance is solvable at all. This post contains some interesting cases that I ran into.

Tile Domination

Typical tile domination. The 2 dominates the upper 1 (sees all tiles of it, plus some more)

Tile domination with very good payoff! The yellow tiles contain exactly one mine.

A nice interdependence between the top three middle tiles, give us that the red tile is a mine. Could also be solved with tile domination between the "1" and one of the "2"s.

Gradient

A hard to spot application of the gradient rule. The yellow tiles must contain exactly one mine.

Another hard to spot gradient, between the middle "1" and the middle "3". The yellow tiles contain exactly one mine. 

Global constraint

(counting total number of mines)

Typical application of the global constraint. The colored area is the only unknown area left in the game. The yellow, orange, and turquoise tiles contain exactly one mine each. Since there are only three mines left in the game, the green tiles must be free.

A larger application of the global constraint. The yellow and orange tiles must contain exactly two mines each. The turquoise tiles contain exactly one mine. Therefore, the green tiles are free.

Applying the global constraint with two remaining separate areas. There is just one way to assign two mines so as to "touch" all unsatisfied tiles. 

 Multi-step inferences

Shared tile domination: the "2" on the lower left must be satisfied by the combined yellow and orange tiles.

Proving that the "box" is filled diagonally. I have marked colored boxes around the tiles that yield the conclusions about the colored tiles. The order of reasoning goes first: yellow, orange, purple, and turquoise must all contain one mine, by straight application of adjacency constraints. Then brown is inferred to contain one mine based on orange, purple, and turquoise. With this, we see that the green tiles are free. 

Yellow, turquoise, and brown fields contain one mine by adjacency constraints. From yellow, we get the orange by tile domination. Using the same reasoning about the box as above, the purple must contain one mine, so the green tiles are free by saturation of the right "1". Using the box in the other direction, the tile directly above the left "3" must be free. 

Minesweeper pt. 2: SAT (the cheating button)

Previous:

• Minesweeper Turbo

In the previous post, I applied some more or less simple rules for playing Minesweeper. At the end of it, two issues were raised. First, we would like to generate only problems that we know are solvable. Second, we would like to check whether a certain situation is truly "impossible", or whether we can make more inferences. Both of these features would be simple if we could automatically exhaust all possible inferences for a certain board. This is what SAT will do for us. 

Implementation

The method of determining whether or not tiles are mines will be proof by contradiction. We will set up a SAT model that holds the adjacency constraints. A tile X can be shown to be a mine by showing that "X is free" leads to the SAT model being unsatisfiable. Likewise, X can be shown to be free by showing that "X is mine" makes the SAT model unsatisfiable. 

Aside from the adjacency constraints, we can also add a global constraint on the total number of mines, since this is known to the player. 

For performance reasons, the only unknown tiles considered will be those that touch an open tile. None other are relevant for the adjacency constraints. 

	# The class of 'self' inherits nx.Graph
	def apply_SAT(self, board):
	while True:
	# Let the trivial rules do the heavy lifting,
	# for speed.
	self.apply_trivial(board)
	solver = SugarRush()
	known_tiles = set([tile for tile in self
	if self.nodes[tile]["mine"] is not None])
	known_dilute = set(flatten([self[tile] for tile in known_tiles]))
	# The rim consists of unknown tiles that touch known tiles.
	rim = known_dilute - known_tiles
	unknown_tiles = set(self.nodes) - known_tiles
	unknown_dilute = set(flatten([self[tile] for tile in unknown_tiles]))
	# The front consists of known tiles that touch unknown tiles.
	front = unknown_dilute - unknown_tiles
	# The decisions we are interested in
	# is what to do with the unknown tiles.
	tile2var = {tile: solver.var() for tile in rim}
	# Cardinality constraints.
	# The number on known tiles must be equal
	# to the number of adjecent mines.
	for tile in front:
	if self.nodes[tile]["adj"] is None: # mine
	continue
	unknown_neigh = self.get_unknown_neigh(tile)
	unknown_neigh = [tile2var[neigh] for neigh in unknown_neigh]
	adj = self.nodes[tile]["adj"]
	flagged_neigh = self.num_mine_neigh(tile)
	remaining_mines = adj - flagged_neigh
	solver.add(solver.equals(unknown_neigh, bound=remaining_mines))
	# Global constraint
	# The total number of mines is known,
	# so we can add a constraint for this too.
	all_vars = [var for var in tile2var.values()]
	remaining_mines = self.S - self.num_mines_total()
	if len(rim) == len(unknown_tiles):
	solver.add(solver.equals(all_vars, bound=remaining_mines))
	else:
	solver.add(solver.atmost(all_vars, bound=remaining_mines))
	for tile in rim:
	# Do reductio ad absurdum on tile values.
	var = tile2var[tile]
	if not solver.solve(assumptions=[var]):
	# Assumption that it's a mine failed -
	# must be free.
	self.sweep(board, tile)
	# New information: go through all unknown tiles again.
	break
	if not solver.solve(assumptions=[-var]):
	# Assumption that it's free failed -
	# must be a mine.
	self.flag(tile)
	# New information: go through all unknown tiles again.
	break
	else:
	# Could not infer any new tiles: exit.
	break

view raw ms_sat.py hosted with ❤ by GitHub

Consequences

Given a method to exhaust all inferences, we can generate solvable instances by running the apply_SAT function to the initial state, and see if it leads to a finished game. If not, generate a new problem and try again. When we are working with a solvable game, we always know that there is at least one way to proceed, at least one tile that can be inferred to be free or a mine. 

For games that are not guaranteed to be solvable, I installed a "cheating button". We can also call it an "answer sheet button". The cheating button runs apply_SAT. If no more tiles open, the situation was actually hopeless.  If some tiles opened, there was something to do. After apply_SAT finishes, however, there is nothing to do. One must simply take a guess. Of course, in Minesweeper we do not care to guess, so mathematically, the game is over. 

Performance

Proving that a given Expert game (16x30 tiles, 99 mines) is unsolvable takes 0.1-1 seconds. Proving that it is solvable is about the same. For a Super-Expert game (30x50 tiles, 300 mines), the time is about 1-10 seconds for proving solvability/unsolvability. Expert games and Super-Expert games are solvable with a rate of about 1 in 10. 

Minesweeper Turbo

Remember minesweeper? You left click to open a tile, and right click to flag it as a mine. When a tile is opened, it displays the number of mines in the 8-connected adjacent tiles. Open a mine and you're dead. You win the game by opening all non-mines.

A finished beginner game: 8x8 tiles, 10 mines.

I started playing it again recently, not having played it for about 10 years. It was fun to attack the game again with a more "adult" brain. More patience and experience with logic inference made it possible to tackle the larger board sizes. However, it also got boring faster. I noticed that most of the work is applying one of two "trivial" rules:

1) A tile is marked with a number X. It is surrounded by X tiles flagged as mines (it is saturated), and at least one unopened tile. Therefore, none of the adjacent unopened tiles are mines, and they can be safely opened.

2) A tile is marked with a number X. It is surrounded by Y tiles flagged as mines (Y may be 0), and exactly Z unopened tiles. Furthermore X = Y + Z. In this case, all of the adjacent tiles are mines, and can be flagged.

Let's illustrate with an example:

Example application of the two "trivial" rules. Rule 2 can be used to infer that the red tiles are mines.
Once that is flagged, rule 1 gives us that all the green tiles are non-mines.
With the extra information gathered thus, the trivial rules can be applied again, and perhaps again...

The trivial rules go a long way. They are often enough to clear the beginner instance. However, for intermediate (16x16 tiles, 40 mines) you must usually do at least one nontrivial inference (1 in about 20 intermediate games I played was cleared by the trivial rules). For expert games (16x30 tiles, 99 mines), I take it as a guarantee that more advanced inference is needed.

But the more advanced inference is the fun part! I want to do more of that, and less of the grunt-work of applying the trivial rules. Solution: write my own implementation of minesweeper, that applies the trivial rules automatically as long as they can be applied.

Implementation

How to represent the state of a minesweeper game? What operations are relevant on the tiles? We want a convenient way to check the neighbours of a tile, so a graph is not out of order. The state of what we know about the tiles can be saved as node attributes, if we use a networkx graph. I use two node attributes: "adj" meaning the number of adjacent mines. If the tile is unopened, "adj" is None. If the tile is flagged, "adj" is also None. The other node attribute is "mine". If the tile is flagged, "mine" is 1. If the tile is opened, "mine" is 0. If the tile is neither opened nor flagged, "mine" is None.

For the game, I use two boards. One "ground truth" board, that is polled when we open new tiles. A "solution" board keeps track of the information known to the player. 

To initiate the game, I ask the ground truth board to provide a random tile with 0 adjacent mines. This is the way I typically start a game: click randomly until I hit a tile with 0 adjacent mines, which will be automatically recursively expanded in the original minesweeper. 

My implementation of exhausting the trivial rules. The class that this method is in inherits nx.Graph.

	def apply_trivial(self, ground_truth):
	while True:
	for node in self.nodes:
	if self.nodes[node]["adj"] is None:
	# Tile is flagged or unopened:
	# trivial rules not applicable.
	continue
	if not self.num_unknown_neigh(node):
	# We already know everything about
	# this tile's neighbours.
	continue
	if self.nodes[node]["adj"] == self.num_mine_neigh(node):
	# Rule 1: We have found all adjacent mines.
	for neigh in self[node]:
	if self.nodes[neigh]["mine"] is None:
	adj = board.open(neigh)
	self.update(neigh, adj)
	# New information: go through all tiles again.
	break
	if self.nodes[node]["adj"] == self.num_mine_neigh(node) \
	+ self.num_unknown_neigh(node):
	# Rule 2: All remaining adjacent tiles are mines.
	for neigh in self[node]:
	if self.nodes[neigh]["mine"] is None:
	# Flag as a mine.
	self.update(neigh, None)
	# New information: go through all tiles again.
	break
	else:
	# We have gone through all tiles and
	# not been able to apply the rules: exit.
	break

view raw ms_trivial.py hosted with ❤ by GitHub

"More implementation details"

Gameplay

Let's look at some of the more "advanced" inferences. Some are not so difficult. What they have in common is that they look at the information in more than one tile. 

Tile Domination

Suppose tile A sees some set of unknown tiles. Suppose that tile B sees a strict subset of A's tiles. This can for example be the case at the edge of the board, as shown below. The "2" sees three tiles and the "1" sees two of them. They are both undersaturated by one mine. We know from the "1" that there must be exactly one mine in the two lower unknown tiles. Therefore, the "2" must be saturated from this, and the remaining tile (marked green) must be safe.

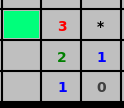Simplest demonstration of the application of the tile domination rule. There must be a mine in one of the two lower of the unknown tiles, which will saturate the "2", so the tile marked green must be safe. 

The same principle can be used to infer that the remaining neighbours of the dominating tile must be all mines, such as below:

Applying tile domination to infer that the remaining neighbours of the domination must be all mines. 

Another application of the tile domination rule:

Another application of the tile domination rule. The yellow tiles are known to contain exactly one mine. Therefore, the green tiles can be inferred to be free. 

An application of the tile domination rule that was not so easy to spot! The yellow tiles contain exactly two mines, so the green tile must be free.

Yet another nontrivial tile domination rule. 

Gradient

In the absence of dominating tile pairs, we can use changes in mine-density along a rim.

Applying the gradient rule. The two tiles marked yellow must contain exactly one mine. If the yellow tiles contained zero mines, the "2" could not be saturated. If they contained two mines, the "1" would be oversaturated. With this knowledge, we can infer one mine to the left, and one free tile to the right. 

The gradient rule can reveal quite a few tiles:

Another application of the gradient rule. The yellow tiles are inferred to contain exactly one mine. With this, the green tiles are known to be free and the red tile is know to be a mine. 

Multi-step applications

Sometimes, applying tile domination and/or gradients does not lead directly to making a tile certain, but can do so indirectly. 

Applying tile domination in two steps. First, the yellow tiles are inferred to contain exactly one mine. Therefore, the orange tiles must contain exactly one mine. With this knowledge, we know that the green tile is free. 

Getting interesting! First, the yellow tiles are inferred to contain exactly one mine. Second, we can infer that the orange tiles must contain at least two mines, by applying gradient to the neighbouring "3" and "1". Therefore, the purple tiles must contain at least one mine. With this, the "2" below the "3" is saturated by the yellow and purple tiles, and the green tiles must be free. 

Beautiful example of a two-step inference. First, the yellow and orange group must contain one mine each. Therefore, the green tile must be free. 

Infinite-step inference?

It can be amusing to come up with rules like this, and make more and more advanced inferences. The frustrating thing is that the game is not always logically solvable, not even if we're able to make an infinite step inference. That is to say, there may not be objectively enough information to avoid guessing, no matter how smart one is. Example:

An objectively impossible case. We know that the yellow tiles contain exactly one mine, but cannot determine which. Note that the bottom right corner is the board's bottom right corner. 

So it would be nice to generate games that we know are solvable. 

Another point of pain is when I can't come up with any inference, but also can't determine that there is objectively too little information. In those cases, I have to hit a tile at random, and don't learn whether there was something I could have done. So it would be nice to be able to "read the answer sheet" to learn exotic rules. 

Can we do these things without solving games automatically? I don't know that, but I know how to solve games automatically! We can model it as a SAT problem. SAT is actually just perfect for this. More on this next time.