Minesweeper Turbo

Remember minesweeper? You left click to open a tile, and right click to flag it as a mine. When a tile is opened, it displays the number of mines in the 8-connected adjacent tiles. Open a mine and you're dead. You win the game by opening all non-mines.

A finished beginner game: 8x8 tiles, 10 mines.

I started playing it again recently, not having played it for about 10 years. It was fun to attack the game again with a more "adult" brain. More patience and experience with logic inference made it possible to tackle the larger board sizes. However, it also got boring faster. I noticed that most of the work is applying one of two "trivial" rules:

1) A tile is marked with a number X. It is surrounded by X tiles flagged as mines (it is saturated), and at least one unopened tile. Therefore, none of the adjacent unopened tiles are mines, and they can be safely opened.

2) A tile is marked with a number X. It is surrounded by Y tiles flagged as mines (Y may be 0), and exactly Z unopened tiles. Furthermore X = Y + Z. In this case, all of the adjacent tiles are mines, and can be flagged.

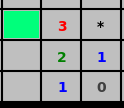
Let's illustrate with an example:

Example application of the two "trivial" rules. Rule 2 can be used to infer that the red tiles are mines.
Once that is flagged, rule 1 gives us that all the green tiles are non-mines.
With the extra information gathered thus, the trivial rules can be applied again, and perhaps again...

The trivial rules go a long way. They are often enough to clear the beginner instance. However, for intermediate (16x16 tiles, 40 mines) you must usually do at least one nontrivial inference (1 in about 20 intermediate games I played was cleared by the trivial rules). For expert games (16x30 tiles, 99 mines), I take it as a guarantee that more advanced inference is needed.

But the more advanced inference is the fun part! I want to do more of that, and less of the grunt-work of applying the trivial rules. Solution: write my own implementation of minesweeper, that applies the trivial rules automatically as long as they can be applied.

Implementation

How to represent the state of a minesweeper game? What operations are relevant on the tiles? We want a convenient way to check the neighbours of a tile, so a graph is not out of order. The state of what we know about the tiles can be saved as node attributes, if we use a networkx graph. I use two node attributes: "adj" meaning the number of adjacent mines. If the tile is unopened, "adj" is None. If the tile is flagged, "adj" is also None. The other node attribute is "mine". If the tile is flagged, "mine" is 1. If the tile is opened, "mine" is 0. If the tile is neither opened nor flagged, "mine" is None.

For the game, I use two boards. One "ground truth" board, that is polled when we open new tiles. A "solution" board keeps track of the information known to the player. 

To initiate the game, I ask the ground truth board to provide a random tile with 0 adjacent mines. This is the way I typically start a game: click randomly until I hit a tile with 0 adjacent mines, which will be automatically recursively expanded in the original minesweeper. 

My implementation of exhausting the trivial rules. The class that this method is in inherits nx.Graph.

"More implementation details"

Gameplay

Let's look at some of the more "advanced" inferences. Some are not so difficult. What they have in common is that they look at the information in more than one tile. 

Tile Domination

Suppose tile A sees some set of unknown tiles. Suppose that tile B sees a strict subset of A's tiles. This can for example be the case at the edge of the board, as shown below. The "2" sees three tiles and the "1" sees two of them. They are both undersaturated by one mine. We know from the "1" that there must be exactly one mine in the two lower unknown tiles. Therefore, the "2" must be saturated from this, and the remaining tile (marked green) must be safe.

Simplest demonstration of the application of the tile domination rule. There must be a mine in one of the two lower of the unknown tiles, which will saturate the "2", so the tile marked green must be safe. 

The same principle can be used to infer that the remaining neighbours of the dominating tile must be all mines, such as below:

Applying tile domination to infer that the remaining neighbours of the domination must be all mines. 

Another application of the tile domination rule:

Another application of the tile domination rule. The yellow tiles are known to contain exactly one mine. Therefore, the green tiles can be inferred to be free. 

An application of the tile domination rule that was not so easy to spot! The yellow tiles contain exactly two mines, so the green tile must be free.

Yet another nontrivial tile domination rule. 

Gradient

In the absence of dominating tile pairs, we can use changes in mine-density along a rim.

Applying the gradient rule. The two tiles marked yellow must contain exactly one mine. If the yellow tiles contained zero mines, the "2" could not be saturated. If they contained two mines, the "1" would be oversaturated. With this knowledge, we can infer one mine to the left, and one free tile to the right. 

The gradient rule can reveal quite a few tiles:

Another application of the gradient rule. The yellow tiles are inferred to contain exactly one mine. With this, the green tiles are known to be free and the red tile is know to be a mine. 

Multi-step applications

Sometimes, applying tile domination and/or gradients does not lead directly to making a tile certain, but can do so indirectly. 

Applying tile domination in two steps. First, the yellow tiles are inferred to contain exactly one mine. Therefore, the orange tiles must contain exactly one mine. With this knowledge, we know that the green tile is free. 

Getting interesting! First, the yellow tiles are inferred to contain exactly one mine. Second, we can infer that the orange tiles must contain at least two mines, by applying gradient to the neighbouring "3" and "1". Therefore, the purple tiles must contain at least one mine. With this, the "2" below the "3" is saturated by the yellow and purple tiles, and the green tiles must be free. 

Beautiful example of a two-step inference. First, the yellow and orange group must contain one mine each. Therefore, the green tile must be free. 

Infinite-step inference?

It can be amusing to come up with rules like this, and make more and more advanced inferences. The frustrating thing is that the game is not always logically solvable, not even if we're able to make an infinite step inference. That is to say, there may not be objectively enough information to avoid guessing, no matter how smart one is. Example:

An objectively impossible case. We know that the yellow tiles contain exactly one mine, but cannot determine which. Note that the bottom right corner is the board's bottom right corner. 

So it would be nice to generate games that we know are solvable. 

Another point of pain is when I can't come up with any inference, but also can't determine that there is objectively too little information. In those cases, I have to hit a tile at random, and don't learn whether there was something I could have done. So it would be nice to be able to "read the answer sheet" to learn exotic rules. 

Can we do these things without solving games automatically? I don't know that, but I know how to solve games automatically! We can model it as a SAT problem. SAT is actually just perfect for this. More on this next time.